SIMULATION EINES ZUFALLSEXPERIMENTES: ZUFALLSLAUF Nr. 2 (Markovkette)
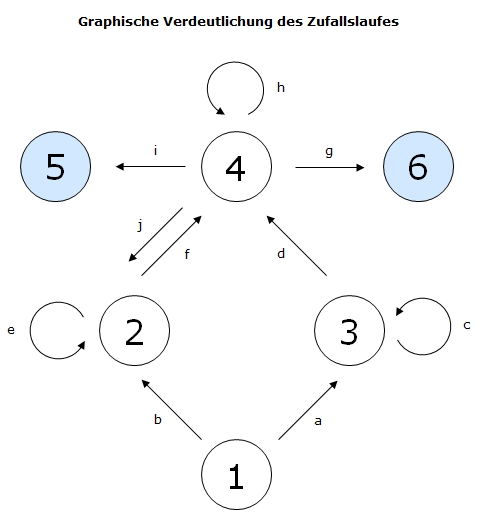
Gegeben sei die durch das Schaubild (vgl. unten) definierte Markovkette, die in den Zuständen 5 und 6 mit der Wahrscheinlichkeit 1 absorbiert.
Man darf sich darunter einen Zufallslauf durch den Graphen unter Beachtung der variabel gehaltenen Übergangswahrscheinlichkeiten vorstellen.
Dieses Programm simuliert das beschriebene Zufallsexperiment, wobei ein jeder Zufallslauf in dem Zustand 1 beginnt, und weist die relative und die absolute Häufigkeit der Fälle aus, in denen der Zufallslauf im Zustand 5 bzw. im Zustand 6 endet.
Die Anzahl der Simulationen und die Übergangswahrscheinlichkeiten a, c, e, g, h und i können vom Benutzer vorgegeben werden.
Dieser kann zudem bestimmen, ob ein vollständiges graphisches Protokoll der Simulation angelegt oder aber lediglich das numerische Endergebnis angezeigt wird.
Für sehr große n kann es im Falle der vollständigen Protokoll-Anzeige zu Browserverzögerungen kommen! Beachte bei der Eingabe der Wahrscheinlichkeiten,
dass diese gewissen Bedingungen genügen müssen! Die Übergangswahrscheinlichkeiten b, d und j werden aus den anderen berechnet.
Bedenke schließlich bei der Betrachtung der ebenfalls ausgewerteten Länge eines Zufallslaufes (Minimum, Maximum und Durchschnitt), dass der Start im Zustand 1 nicht als Schritt gilt: der Lauf 1-3-4-2-4-6 hat also zum Beispiel die Länge 5.